Exercice : Calcul du rapport de transmission d'un train épicycloïdal
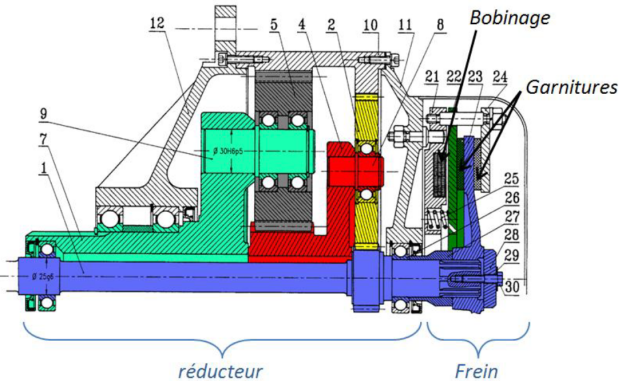
Le réducteur étudié ci-après fait partie d'un système de treuil d'un pont roulant.
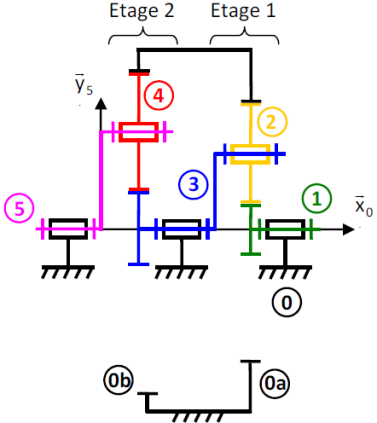
Un modèle cinématique simple a été établi. On définit \(6\) classes d'équivalence, de \(0\) à \(5\).
L'entrée du mouvement se fait par la classe d'équivalence \(1\), la sortie du réducteur complet se fait par la classe d'équivalence \(5\).
Nombre de dents | |
|---|---|
Pignon 1 | 21 |
Roue 2 | 51 |
Couronne 0a | 123 |
Pignon 3 | 23 |
Roue 4 | 34 |
Couronne 0b | 91 |
Question
En appliquant la formule de Willis, déterminer de manière littérale le rapport de transmission de chaque étage du réducteur, puis le rapport global.
Effectuer enfin l'application numérique.
Solution
Etage 1
Planétaire entrée \(1\), planétaire sortie \(0a\), satellite \(2\) et porte satellite \(3\).
\(Willis : \frac{\omega_{0a/3}}{\omega_{1/3}}=-\frac{Z_1.Z_2}{Z_2.Z_{0a}}=-\frac{Z_1}{Z_{0a}}\)
Véritable entrée \(1\), véritable sortie \(3\), bâti \(0a\).
\(\frac{-\omega_{3/0a}}{\omega_{1/0a}-\omega_{3/0a}}=-\frac{Z_1}{Z_{0a}}\) donc \(Z_{0a} \ . \ \omega_{3/0a} = Z_1 \ . \ \left( \omega_{1/0a}-\omega_{3/0a}\right)\)
ce qui donne \(\frac{\omega_{3/0a}}{\omega_{1/0a}}=\frac{Z_1}{Z_1+Z_{0a}}\)
Etage 2
Planétaire entrée \(3\), planétaire sortie \(0b\), satellite \(4\) et porte satellite \(5\).
\(Willis : \frac{\omega_{0b/5}}{\omega_{3/5}}=-\frac{Z_3.Z_4}{Z_4.Z_{0b}}=-\frac{Z_3}{Z_{0b}}\)
Véritable entrée \(3\), véritable sortie \(5\), bâti \(0b\).
\(\frac{-\omega_{5/0b}}{\omega_{3/0b}-\omega_{5/0b}}=-\frac{Z_3}{Z_{0b}}\) donc \(Z_{0b} \ . \ \omega_{5/0b} = Z_3 \ . \ \left( \omega_{3/0b}-\omega_{5/0b}\right)\)
ce qui donne \(\frac{\omega_{5/0b}}{\omega_{3/0b}}=\frac{Z_3}{Z_3+Z_{0b}}\)
Total
Le rapport de transmission total est le produit des rapports précédents.
\(r=\frac{Z_1 Z_3}{(Z_1 +Z_{0a})(Z_3 +Z_{0b})}\) soit environ \(0,029\).