Base et repère
Définition : Base
Dans un espace vectoriel à trois dimensions, le triplet \((\vec e_1, \vec e_2, \vec e_3)\) de vecteurs linéairement indépendants désigne une base (\(b_1\), par exemple).
Elle est dite orthogonale si les produits scalaires des vecteurs pris deux à deux sont nuls :
\(\vec e_i \cdot \vec e_j = 0\), \(\forall (i,j) \in (1,2,3)\) avec \(i \ne j\)
Elle est dite orthonormée si, en plus, la norme des vecteurs vaut 1 :
\(\forall (i,j) \in (1,2,3)\), \(\| \vec e_i \| = 1\)
Elle est dite orthonormée directe si enfin \((\vec e_1, \vec e_2, \vec e_3)\) forme un trièdre direct (c'est-à-dire si \(\vec e_3 = \vec e_1 \wedge \vec e_2\))
Fondamental : Trois doigts de la main droite
Une astuce simple pour vérifier si un trièdre est direct, est d'utiliser les trois doigts de la main droite. Dans l'ordre de lecture du triplet de vecteurs, par exemple \((\vec i, \vec j, \vec k)\) :
le premier vecteur \(\vec i\) est associé au pouce
le deuxième vecteur \(\vec j\) est associé à l'index
le troisième vecteur \(\vec k\) est associé au majeur, qui se déploie perpendiculairement au plan formé par le pouce et l'index.
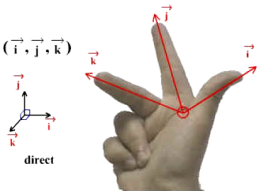
Attention :
Ne pas se tromper de main : la main gauche donnerait un trièdre indirect !
Définition : Repère
En associant un point (par exemple A) à cette base, on obtient un repère \((A, \vec e_1, \vec e_2, \vec e_3)\), aussi noté \((A, b_1)\).