Vecteurs
Définition : Vecteur libre
Soient \(A\) et \(B\), deux points de l'espace. Le vecteur libre \(\overrightarrow {AB} = \vec V\) désigne l'un des bipoints équivalents au bipoint \((A,B)\).
Il est caractérisé par :
une direction
un sens
une norme, ou intensité, ou module
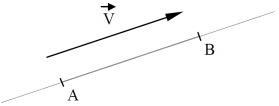
Définition : Vecteur glissant
Le vecteur glissant \((A, \vec V)\) désigne l'un des bipoints équivalents au bipoint \((A,B)\) qui ont la même droite support que \((A,B)\).
Il est caractérisé par :
un support (une direction et un point)
un sens
une norme
L'ensemble des vecteurs glissants est appelé glisseur.
Définition : Vecteur lié
Le vecteur lié \([\vec V]\) est le représentant du bipoint \((A,B)\) qui a pour origine \(A\).
Il est caractérisé par :
une origine
une direction
un sens
une norme
Définition : Norme
La norme d'un vecteur est notée \(||\overrightarrow{AB}||\) et est positive.
Conseil : Obtention efficace de la norme d'un vecteur
On obtient très facilement la norme d'un vecteur en calculant la racine carré du produit scalaire du vecteur avec lui-même : \(||\overrightarrow{AB}||=\sqrt{\overrightarrow{AB}\ . \ \overrightarrow{AB}}\)