Modélisation plane
Définition : Mouvement plan
Le mouvement d'un solide \(S_2\) par rapport à un solide \(S_1\) est dit plan s'il existe un plan \(P_2\) lié à \(S_2\) qui reste coïncident avec un plan \(P_1\) lié à \(S_1\) au cours du mouvement.
Fondamental : Conséquences du mouvement plan
Le paramétrage du solide \(S_2\) par rapport au solide \(S_1\) ne nécessite alors que trois paramètres : deux translations dans le plan et une rotation d'axe perpendiculaire au plan.
Modèles de liaisons planes
En analysant les mouvements entre les solides qui constituent un mécanisme plan, on peut définir un schéma "de mouvement" à l'aide des symboles suivants :
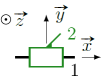
la liaison glissière qui permet un mouvement de translation (ci-contre le symbole dans le plan de la liaison glissière de direction \(\vec x\))
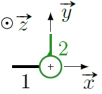
la liaison pivot qui permet un mouvement de rotation (d'axe perpendiculaire au plan), on parle généralement d'
« articulation en un point »
(ci-contre, le symbole d'une liaison pivot d'axe orthogonal au plan du mouvement)
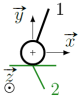
la liaison ponctuelle (sphère-plan) qui permet à la fois un mouvement de translation dans le plan et un mouvement de rotation d'axe perpendiculaire au plan (ci-contre, le symbole dans le plan d'une liaison ponctuelle permettant une translation suivant l'axe \(\vec x\))
Attention :
En modélisation plane uniquement :
on ne tient pas compte de la géométrie des contacts
on représente les mouvements relatifs entre deux pièces dans le plan d'étude.
Le schéma établi est donc un schéma de mouvement, utile pour simplifier l'étude théorique. Il utilise les symboles des liaisons normalisées, non pas comme tels, mais pour définir des mouvements relatifs. C'est là toute l'ambiguïté : cela demande beaucoup de vigilance.