Notion d'appartenance d'un point à un solide
Dès que l'on étudie le mouvement des solides (autrement dit des pièces d'un mécanisme, donc la plupart du temps), il faut savoir si les points dont on exprime la vitesse ou l'accélération font partie d'un solide ou d'un autre, ou d'aucun en particulier !
Notation
On va donc ajouter l'information d'appartenance du point avec le symbole \(\in\) :
\(\overrightarrow{V(P \in 1/0)}\) est le vecteur vitesse du point \(P\) appartenant au solide \(1\), par rapport au repère (ou solide) \(0\) (à la date \(t\))
\(\overrightarrow{\Gamma (P \in 1/0)}\) est le vecteur accélération du point \(P\) appartenant au solide \(1\), par rapport au repère (ou solide) \(0\) (à la date \(t\))
Fondamental : Appartenance naturelle ou supposée
Soit un point \(M\) appartenant naturellement à un solide \(2\).
On peut très bien être amené à exprimer la vitesse ou l'accélération de ce point \(M\), en le supposant appartenant (à l'instant t !) à un autre solide, par exemple \(1\).
Ces vecteurs vitesse ou accélération seront notés également \(\overrightarrow{V(M \in 1/0)}\) ou \(\overrightarrow{\Gamma (M \in 1/0)}\).
La notation ne permettra donc pas de savoir si le point considéré appartient naturellement ou non au solide indiqué.
Exemple : Deux roues lisses en contact
Soient deux roues lisses \(1\) et \(2\), en contact au point \(I\), tournant l'une contre l'autre (sans glissement) respectivement selon les axes fixes de rotation \((A, \vec z_0)\) et \((O, \vec z_0)\). Le repère de référence \(R_0(O, \vec x_0, \vec y_0, \vec z_0)\) est lié au bâti \(0\).
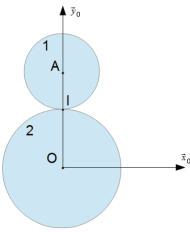
Plusieurs vitesses du point \(I\) peuvent être considérées :
celle du point \(I\) appartenant à la roue \(1\), par rapport au repère \(0\) : \(\overrightarrow{V(I \in 1/0)}\)
celle du point \(I\) appartenant à la roue \(2\), par rapport au repère \(0\) : \(\overrightarrow{V(I \in 2/0)}\)
celle du point \(I\) n'appartenant à aucun solide, par rapport au repère \(0\) : \(\overrightarrow{V(I/0)}\)
La troisième vitesse, \(\overrightarrow{V(I/0)}\) (sans appartenance particulière spécifiée, donc concernant le point de contact situé géométriquement sur la figure) est par définition la dérivée du vecteur position \(\overrightarrow{OI}\).
On se rend compte rapidement que cette vitesse est ici nulle, alors que \(\overrightarrow{V(I \in 1/0)}\) et que \(\overrightarrow{V(I \in 2/0)}\) ne le sont pas !
Fondamental : Dériver un vecteur position pour obtenir la vitesse d'un point
Dressons un bilan à propos de la vitesse d'un point obtenue par dérivation d'un vecteur position.
La formule suivante n'est valable qu'à deux conditions :
le point \(A\) est fixe dans le repère \(1\)
le point \(B\) est fixe dans le repère \(2\)
Si l'une de ces deux conditions n'est pas valable, il faut utiliser la composition des vitesses ou la relation de Varignon pour déterminer la vitesse recherchée.