Détail du calcul d'un rapport de transmission d'un train épicyloïdal
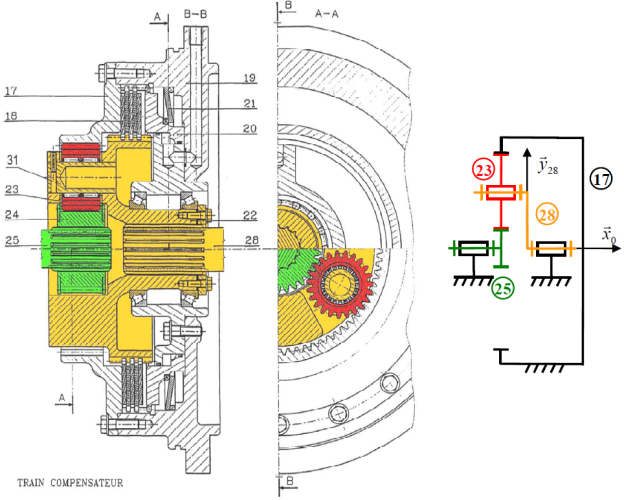
Voici un train épicycloïdal utilisé dans un bulldozer.
Le mouvement d'entrée se fait par la roue \(25\), celui de sortie par l'arbre \(28\), qui est également le porte satellites. Les satellites sont représentés par la roue \(23\). La couronne \(17\) est fixée au bâti.
Le planétaire de "sortie" est difficile à concevoir, on procède par déduction : le planétaire d'entrée est la roue \(25\). Le planétaire de "sortie" est donc la couronne \(17\) (c'est le seul autre planétaire).
Il n'y a qu'un contact extérieur (entre le planétaire \(25\) et le satellite \(23\)).
Méthode : Première étape : application de la formule de Willis
\(\displaystyle{\frac{\omega_{\text{planétaire de "sortie" / porte-satellites}}}{\omega_{\text{planétaire d' "entrée" / porte-satellites}}} = \frac{\omega_{17/28}}{\omega_{25/28}} =(-1)^1 \ . \ \frac{Z_{25}.Z_{23}}{Z_{23}.Z_{17}}}\)
Il semble étrange que \(17\) soit une roue menée. Le plus facile est de penser à un "chemin pris" par la puissance depuis l'entrée :
la puissance "entre" par la roue \(25\), qui est donc menante
elle mène alors le satellite \(23\), qui est alors mené
le satellite devient ensuite menant, puisqu'il est en contact avec une autre roue
cette dernière roue est la couronne \(17\), qui est donc menée.
Ainsi \(\displaystyle{\frac{\omega_{17/28}}{\omega_{25/28}} =-\frac{Z_{25}}{Z_{17}}}\)
Remarque :
Ici les nombres de dents des satellites ont disparu : c'est uniquement dû au fait qu'ils n'ont qu'une seule denture, à la fois menante et menée. Mais dans beaucoup d'autres types de trains épicyloïdaux, ce n'est pas le cas !
Méthode : Deuxième étape : définition du véritable rapport de transmission
Le véritable rapport de transmission doit s'établir en pensant à identifier :
quelle pièce est la véritable sortie (ici \(28\))
quelle pièce est la véritable entrée (ici \(25\))
quelle pièce est le bâti fixe (ici \(17\))
Le rapport de transmission étant le rapport des vitesses de sortie sur entrée, toutes deux exprimées par rapport au bâti, cela donne ici : \(\displaystyle{r=\frac{\omega_{28/17}}{\omega_{25/17}}}\).
Méthode : Troisième étape : manipulation de la formule de Willis afin d'obtenir le rapport de transmission
Par composition des vitesses, l'idée est de faire apparaître les deux vitesses définissant le rapport de transmission : \(\displaystyle{\frac{\omega_{17/28}}{\omega_{25/28}} = \frac{-\omega_{28/17}}{\omega_{25/17}+\omega_{17/28}} =\frac{-\omega_{28/17}}{\omega_{25/17}-\omega_{28/17}}}\)
Ensuite on relie au rapport des nombres de dents, et on manipule l'équation :
\(\displaystyle{\frac{-\omega_{28/17}}{\omega_{25/17}-\omega_{28/17}}=-\frac{Z_{25}}{Z_{17}}}\) donc \(Z_{17}.\omega_{28/17} = Z_{25}.\left(\omega_{25/17}-\omega_{28/17}\right)\)
soit \(\left(Z_{17}+Z_{25}\right).\omega_{28/17} = Z_{25}.\omega_{25/17}\)
On obtient ainsi : \(\displaystyle{r=\frac{\omega_{28/17}}{\omega_{25/17}}=\frac{Z_{25}}{Z_{25}+Z_{17}}}\)