Étude cinématique
Principe
Chaque roue menante d'un engrenage entraîne une roue menée grâce à des dents au profil en développante de cercle assurant le roulement sans glissement de deux cylindres fictifs appelés "cylindres primitifs".
Lorsque la roue \(2\) engrène avec la roue \(3\), les cercles primitifs des roues roulent l'un sur l'autre sans glisser au point \(I\).
Les roues \(2\) et \(3\) sont placées en liaison pivot avec un bâti \(1\).
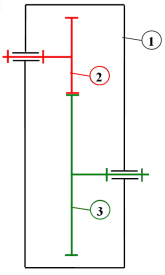
Roulement sans glissement
Les roues \(2\) et \(3\) étant en rotation de centre \(O_2\) et \(O_3\) par rapport à \(1\), on peut écrire : \(\overrightarrow{V(M_2\in 2/1)} = R_2\ \dot \theta_2 \ \vec y_2\) et \(\overrightarrow{V(M_3\in 3/1)} = R_3\ \dot \theta_3 \ \vec y_3\) .
La condition de roulement sans glissement permet d'écrire également : \(\overrightarrow{V(I\in 2/3)} = \vec 0\).
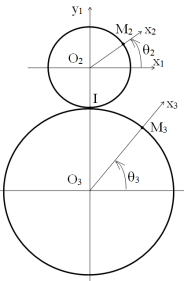
On obtient le rapport de réduction \(\displaystyle{\frac{\dot \theta_3}{\dot \theta_2} = \frac{\omega_3}{\omega_2} = - \frac{R_2}{R_3}}\).
Complément : Démonstration
\(\overrightarrow{V(I\in 2/3)} = \vec 0 = \overrightarrow{V(I\in 2/1)} - \overrightarrow{V(I\in 3/1)} \).
Or :
\(\overrightarrow{V(I\in 2/1)} = \overrightarrow{V(O_2\in 2/1)} + \overrightarrow{IO_2} \wedge \overrightarrow{\Omega(2/1)}=R_2 \vec y_1 \wedge \dot \theta_2 \vec z = R_2 \dot \theta_2 \vec x_1\)
\(\overrightarrow{V(I\in 3/1)} = \overrightarrow{V(O_3\in 3/1)} + \overrightarrow{IO_3} \wedge \overrightarrow{\Omega(3/1)}=-R_3 \vec y_1 \wedge \dot \theta_3 \vec z = - R_3 \dot \theta_3 \vec x_1\)
Ainsi : \(R_2 \dot \theta_2 = - R_3 \dot \theta_3\) soit \(\displaystyle{\frac{\dot \theta_3}{\dot \theta_2} = - \frac{R_2}{R_3}}\).
Remarque : Contact intérieur ou extérieur
Si les deux roues sont en contact extérieur, comme dans l'exemple précédent, il y inversion du sens de rotation, donc un rapport de réduction négatif.
Si les deux roues sont en contact intérieur, le sens de rotation ne change pas, et le rapport de réduction est positif.
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Complément : Train d'engrenages
Impossible d'accéder à la ressource audio ou vidéo à l'adresse :
La ressource n'est plus disponible ou vous n'êtes pas autorisé à y accéder. Veuillez vérifier votre accès puis recharger la vidéo.
Fondamental : Rapport de transmission d'un train d'engrenage simple
où :
\(n\) = nombre de contacts extérieurs (où les roues en contact sont à l'extérieur l'une de l'autre, ce qui inverse le sens de rotation)
\(Z\) = nombre de dents