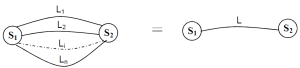Graphe des liaisons
Définition :
Le graphe des liaisons est une représentation plane décrivant les liaisons entre les pièces d'un mécanisme. Dans l'optique d'une étude des mouvements ou des conditions d'équilibre, les solides sont regroupés par classes d'équivalence.
Ainsi, le graphe des liaisons se compose :
de cercles symbolisant les classes d'équivalence
d'arcs de courbe, joignant certains des cercles, symbolisant les liaisons
Exemple :
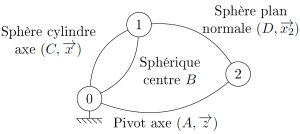
Dans cet exemple, le mécanisme est constitué de trois classes d'équivalence numérotées 0 à 2, et de quatre liaisons.
Attention :
Les liaisons doivent être décrites de manière exhaustive : nom et caractéristique géométrique.
Liaisons en parallèle
Définition :
Plusieurs liaisons sont disposées en parallèle entre deux solides 1 et 2 si chacune relie directement les deux solides.
Liaison équivalente
La liaison équivalente à l'ensemble des liaisons en parallèle entre les solides 1 et 2 est la liaison théorique qui autorise le même mouvement relatif entre les deux solides.
Liaisons en série
Définition :
Plusieurs liaisons sont en série (ou réalisent une chaîne ouverte) entre deux solides 0 et n, si elles sont disposées l'une à la suite de l'autre par l'intermédiaire de (n-1) solides.
Liaison équivalente
La liaison équivalente à l'ensemble des liaisons en série entre les solides 0 et n est la liaison théorique qui autorise le même mouvement relatif entre les deux solides.
Graphe minimal des liaisons
Remarque :
En remplaçant dans le graphe des liaisons d'un mécanisme les liaisons en parallèle et les liaisons en série par leur liaison équivalente (plusieurs fois de suite si possible), de façon à ne conserver que les pièces principales du mécanisme, on obtient le graphe minimal des liaisons.