Bases 1 et 2 : exemple simple
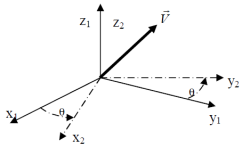
On considère deux bases déduites l'une de l'autre par une rotation autour d'un des vecteurs. Ici la rotation se fait autour de \(\vec z_1 = \vec z_2\) avec l'angle \(\theta\).
Ainsi : \(\theta = (\vec x_1, \vec x_2) = (\vec y_1, \vec y_2)\).
Méthode : Changement de base par projection orthogonale
Chaque vecteur unitaire de la base \(b_1\) peut être exprimé dans la base \(b_2\), et vice-versa.
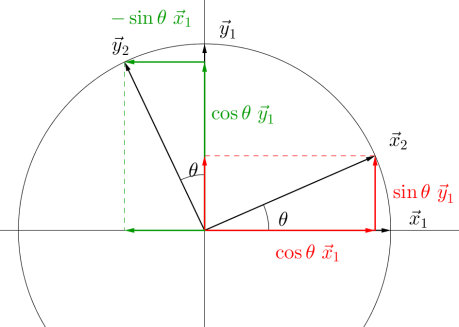
Il est utile de se représenter mentalement le cercle trigonométrique (ici dans le plan \((\vec x_1, \vec y_1)\)) où tous les vecteurs des bases, étant unitaires, auront leur extrémité sur le cercle de rayon 1.
La projection orthogonale va consister à remplacer un vecteur d'une base par la somme de deux vecteurs orthogonaux appartenant à l'autre base. L'ensemble des trois vecteurs tracés fera penser à un triangle rectangle où :
le vecteur projeté correspondra à l’hypoténuse
les deux vecteurs sommés correspondront aux côtés adjacent et opposé.
Par exemple : \(\vec x_2\) sera remplacé par \(\cos \theta \vec x_1 + \sin \theta \vec y_1\).