Composantes scalaires d'un vecteur dans l'espace
On peut exprimer un vecteur à l'aide d'une combinaison linéaire de ses composantes scalaires dans cette base.
en coordonnées cartésiennes
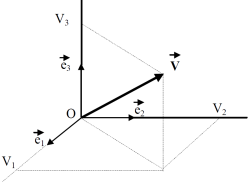
\(\vec V = V_1 \ \vec e_1 + V_2 \ \vec e_2 + V_3 \ \vec e_3\)
Syntaxe : Écriture "colonne" d'un vecteur
Afin d'écrire de manière concise et détaillée un vecteur grâce à ses composantes, on utilise la présentation suivante : \(\vec V = \left\{ \begin{array}{c} V_1 \\ V_2 \\ V_3\end{array}\right\}_{b_1}\) , ou \(\vec V = {\begin{array}{c} \\ \\ \\ \end{array}}_{b_1} \left| \begin{array}{c} V_1 \\ V_2 \\ V_3\end{array}\right.\)
\(V_1\), \(V_2\) et \(V_3\) sont appelées les coordonnées du vecteur V.
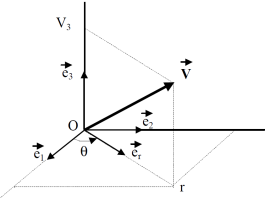
en coordonnées cylindriques
\(\\\)
\(\vec V = r \ \vec e_r + V_3\ \vec e_3\)
Remarque :
\(\vec e_r\) est de norme unitaire mais n'est pas fixe par rapport à la base \(b_1\).
en coordonnées sphériques
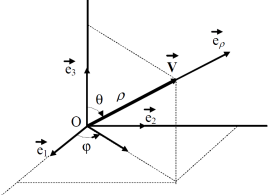
\(\vec V = \rho \ \vec e_{\rho}\)
Remarque :
\(\vec e_{\rho}\) est de norme unitaire mais n'est pas fixe par rapport à la base \(b_1\).