Composition des vecteurs vitesse
Soient deux solides \(S_1\) (repère \(R_1\)) et \(S_2\) (repère \(R_2\)) en mouvement l'un par rapport à l'autre et en mouvement par rapport au repère \(R_0\).
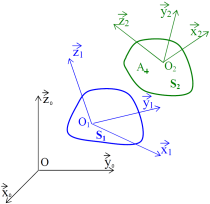
Composition des vecteurs vitesse instantanée
Comme :
\(A\) est un point qui appartient naturellement au solide \(2\)
\(O\) est un point fixe dans \(0\)
on peut écrire \(\overrightarrow{V(A\in 2/0)} = \left[ \frac{d \overrightarrow{OA}}{dt}\right]_0 = \left[ \frac{d \overrightarrow{OO_1}}{dt}\right]_0 + \left[ \frac{d \overrightarrow{O_1 A}}{dt}\right]_0\)
Or :
\(\left[ \frac{d \overrightarrow{OO_1}}{dt}\right]_0 = \overrightarrow{V(O_1\in 1/0)}\) car \(O_1\) est un point fixe pour le solide \(1\)
\(\left[ \frac{d \overrightarrow{O_1 A}}{dt}\right]_0 = \left[ \frac{d \overrightarrow{O_1 A}}{dt}\right]_{1} + \overrightarrow{\Omega(1/0)} \wedge \overrightarrow{O_1 A}\)
Enfin :
\(\left[ \frac{d \overrightarrow{O_1 A}}{dt}\right]_{1} = \overrightarrow{V(A\in 2 /1)}\) car \(O_1\) est un point fixe pour le solide \(1\)
\(\overrightarrow{V(O_1\in 1 /0)} + \overrightarrow{\Omega(1/0)} \wedge \overrightarrow{O_1A} = \overrightarrow{V(A\in 1 /0)}\) (formule de changement de point)
Définition :
Remarque :
Dans le mouvement du point \(A\) appartenant (naturellement) au solide \(2\) par rapport au repère \(0\), on parle souvent de :
vitesse absolue \(\overrightarrow{V(A\in2/0)}\)
vitesse relative \(\overrightarrow{V(A\in2/1)}\)
vitesse d'entraînement \(\overrightarrow{V(A\in1/0)}\) (car c'est la vitesse du point \(A\) comme s'il était entraîné par \(1\) dans son mouvement par rapport à \(0\))
Composition des vecteurs rotation
En appliquant la formule de Bour à un vecteur \(\vec U\) quelconque, avec trois repères différents \(0\), \(1\) et \(2\) :
\(\left[ \frac{d \vec U}{dt} \right]_{2} = \left[ \frac{d \vec U}{dt} \right]_{1} + \overrightarrow{\Omega(1 / 2)} \wedge \vec U\)
\(\left[ \frac{d \vec U}{dt} \right]_{1} = \left[ \frac{d \vec U}{dt} \right]_{0} + \overrightarrow{\Omega(0 / 1)} \wedge \vec U\)
\(\left[ \frac{d \vec U}{dt} \right]_{0} = \left[ \frac{d \vec U}{dt} \right]_{2} + \overrightarrow{\Omega(2 / 0)} \wedge \vec U\)
et en additionnant les trois équations obtenues, on obtient quel que soit \(\vec U\) :
\(\overrightarrow{\Omega(1/2)} \wedge \vec U + \overrightarrow{\Omega(0/1)} \wedge \vec U +\overrightarrow{\Omega(2/0)} \wedge \vec U = \vec 0\)
Définition :
Composition des torseurs cinématiques
On peut déduire des points précédents la relation de composition des vecteurs cinématiques (exprimés bien entendu au préalable au même point) :