Mouvement relatif de deux solides en contact ponctuel
Soient deux solides \(1\) et \(2\) en contact ponctuel en un point \(P\), et (\(\pi\)) le plan tangent commun en \(P\) aux deux solides.
Le torseur cinématique du mouvement du solide \(1\) par rapport au solide \(2\) s'écrit au point \(P\) :
\(\left\{ \mathcal{V}(1/2) \right\} = \begin{array}{c}\\ \\ \\ \end{array}_P \left\{ \begin{array}{c} \overrightarrow{\Omega(1/2)}\\ \overrightarrow{V(P\in 1/2)}\end{array} \right\}\)
Définition : Vecteur vitesse de glissement
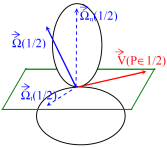
\(\overrightarrow{V(P\in 1/2)}\) est appelé vecteur vitesse de glissement au point \(P\) du solide \(1\) par rapport au solide \(2\).
Il est situé dans le plan tangent commun (\(\pi\)) en \(P\) à \(1\) et \(2\).
Le vecteur vitesse de rotation \(\overrightarrow{\Omega(1/2)}\) peut être décomposé en :
vecteur de pivotement \(\overrightarrow{\Omega_n (1/2)}\)
vecteur de roulement \(\overrightarrow{\Omega_t (1/2)}\):
Fondamental :
Si \(\overrightarrow{V(P\in 1/2)} = \vec 0\), on dit que 1 roule (et pivote) sans glisser sur 2.