Exercice : Vecteurs et opérations vectorielles
Soit \(R (O ; \vec x, \vec y, \vec z)\) un repère orthonormé direct. Les vecteurs \(\vec v\) et \(\vec u\) sont des vecteurs unitaires définis dans le plan \((O; \vec y, \vec z)\) comme le montre la figure ci-dessous :
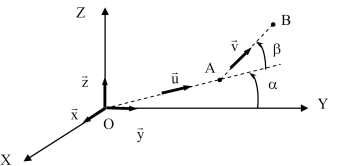
Le vecteur \(\overrightarrow{OA}\) est défini par : \(\overrightarrow{OA}=a \vec u\), et le vecteur \(\overrightarrow{AB}\) par \(\overrightarrow{AB}=b \vec v\).
Question
Définir les coordonnées du vecteur \(\overrightarrow{OB}\) dans la base \((\vec x, \vec y, \vec z)\) en fonction de \(a\), \(b\), \(\alpha\) et \(\beta\).
Question
Déterminer la norme du vecteur \(\overrightarrow{OB}\).
Question
Définir l'angle \(\gamma\) tel que \(\gamma=(\vec y, \overrightarrow{OB})\).
Question
Calculer : \(\overrightarrow{OA}\wedge\overrightarrow{AB}\), \(\vec x \wedge \vec u\), \(\vec y \wedge \vec v\), et \((\overrightarrow{OA} \wedge \overrightarrow{OB}).\vec x\).