Vecteurs

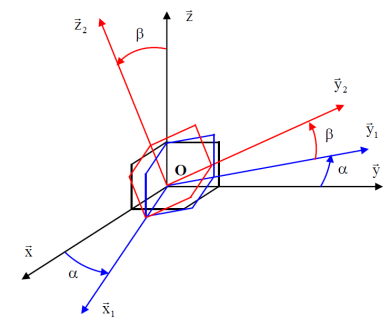
Soit \(R (O ; \vec x, \vec y, \vec z)\) un repère orthonormé direct. La base \((\vec x_1, \vec y_1, \vec z)\) est définie par une rotation de la base \((\vec x, \vec y, \vec z)\) autour de \(\vec z\) d'un angle \(\alpha\) (défini positif). La base \((\vec x_1, \vec y_2, \vec z_2)\) est définie par une rotation de la base \((\vec x_1, \vec y_1, \vec z)\) autour de \(\vec x_1\) d'un angle \(\beta\) (défini positif).