Exercice : Pertinence du choix de la base
Soient les bases \(B(\vec x, \vec y, \vec z)\), \(B_1 (\vec x_1, \vec y_1, \vec z)\) et \(B_2 (\vec x_2, \vec y_1, \vec z_2)\).
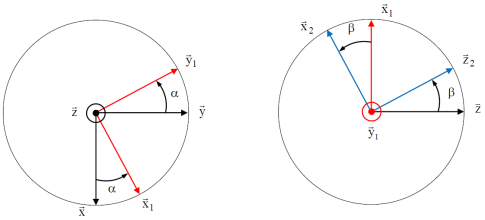
Question
Calculer \(\vec x \wedge \vec x_2\), \(\vec y \wedge \vec x_2\) et \(\vec y_1 \wedge \vec x_2\).
Question
Calculer \((\vec x \wedge \vec x_2).\vec z_2\).
Question
Soit la relation vectorielle suivante : \(a \vec x_2 - b \vec y_1 - c \vec z_2 = \vec 0\) (1).
Donner le système d'équations scalaires issu de la projection de l'équation vectorielle (1) dans la base \(B\).
Donner le système d'équations scalaires issu de la projection de l'équation vectorielle (1) dans la base \(B_2\).
Conclure.