Produit mixte
Définition :
Le produit mixte de \(\vec U\), \(\vec V\) et \(\vec W\) est le nombre réel \([\vec U, \vec V, \vec W]\) tel que :
Propriétés
Invariance par permutation circulaire : \(\left[\vec U, \vec V, \vec W\right] = \left[\vec V, \vec W, \vec U\right] = \left[\vec W, \vec U, \vec V\right]\)
(Antisymétrie par permutation non-circulaire)
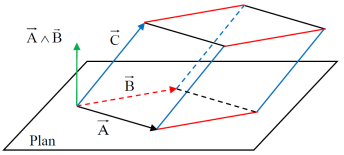
Remarque : Lien entre produit mixte et volume d'un parallélépipède
Soient trois vecteurs (non nuls et non colinéaires) \(\vec A\), \(\vec B\) et \(\vec C\). Le volume du parallélépipède formé par ces trois vecteurs est donné par \(V=|(\vec A \wedge \vec B).\vec C|\)
Fondamental :
Soient les vecteurs non nuls \(\vec U\), \(\vec V\) et \(\vec W\) : si \(\left( \vec U \wedge \vec V \right).\vec W = 0\) alors les trois vecteurs sont coplanaires.
En effet : le vecteur \(\vec U \wedge \vec V\) est (par définition du produit vectoriel) perpendiculaire au plan formé par \(\vec U\) et \(\vec V\). Et si son produit scalaire avec \(\vec W\) est nul, c'est que \(\vec W\) lui est perpendiculaire. Donc ce dernier appartient au plan formé par \(\vec U\) et \(\vec V\).