Produit vectoriel
Définition :
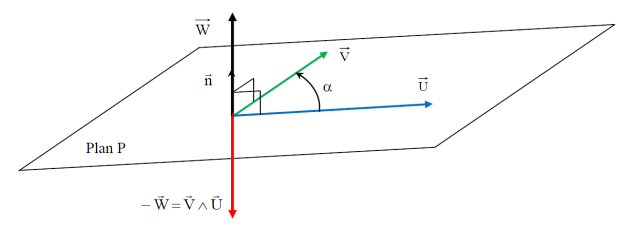
Le produit vectoriel de \(\vec U\) et \(\vec V\) est le vecteur \(\vec W = \vec U \ \wedge \ \vec V\) tel que :
\(\vec W\) est orthogonal à \(\vec U\) et à \(\vec V\)
\(\vec U\), \(\vec V\) et \(\vec W\) forment un trièdre direct.
Propriétés
Antisymétrie : \(\vec U \wedge \vec V = - \vec V \wedge \vec U\)
Bilinéarité : \(\vec U \wedge (\vec V + \vec W) = \vec U \wedge \vec V + \vec U \wedge \vec W\)
Multiplication par un scalaire : \(k (\vec U \wedge \vec V) = (k \ \vec U)\wedge\vec V = \vec U \wedge (k \ \vec V)\)
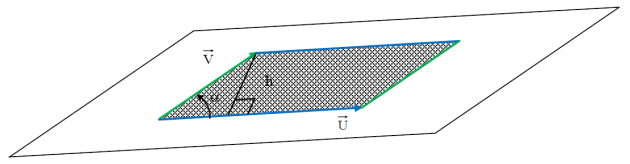
Remarque : Lien entre produit vectoriel et aire d'un parallélogramme
La norme du produit vectoriel \(|| \vec U \wedge \vec V ||\) correspond à l'aire du parallélogramme défini par les vecteurs \(\vec U\) et \(\vec V\) :
\(|| \vec U \wedge \vec V || = ||\vec U||.||\vec V||.|\sin \alpha| = ||\vec U||.h\)
Avec les coordonnées des vecteurs exprimées dans une base orthonormée (rare en SII)
\(\vec U \wedge \vec V = (U_2 . V_3 - U_3 . V_2) \ \vec e_1 +(U_3 . V_1 - U_1 . V_3) \ \vec e_2 + (U_1 . V_2 - U_2 . V_1) \ \vec e_3\)
Fondamental :
Si le produit vectoriel est nul, alors \(\vec U = \vec 0\), ou \(\vec V = \vec 0\),
ou \(\sin (\vec U, \vec V) = 0\) c'est-à-dire que \(\vec U\) et \(\vec V\) sont colinéaires.