Paramétrage de l'orientation de la base
Il reste à définir les paramètres qui permettent d'orienter la base \(b_1(\vec x_1, \vec y_1, \vec z_1)\) par rapport à la base \(b(\vec x, \vec y, \vec z)\).
Complément : En théorie : les angles d'Euler
Trois angles seulement suffisent à donner n'importe quelle orientation à la base \(b_1\) par rapport à la base \(b_0\).
Les angles d'Euler correspondent à un paramétrage possible :
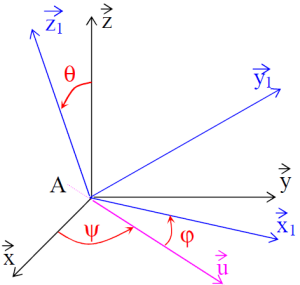
angle "de précession" \(\psi\) permettant la rotation autour de \(\vec z\), pour amener \(\vec x\) sur \(\vec u\)
angle "de nutation" \(\theta\) permettant la rotation autour de \(\vec u\), pour amener \(\vec z\) sur \(\vec z_1\)
angle "de rotation propre" \(\varphi\) permettant la rotation autour de \(\vec z_1\), pour amener \(\vec u\) sur \(\vec x_1\).
Dans la pratique, les angles d'Euler seront très rarement utilisés.
La réalisation technologique d'un mécanisme fait que l'orientation d'un solide 1 par rapport à un solide 0 résultera d'une succession de liaisons engendrant des rotations, et dont les axes seront clairement identifiés.
Ainsi, l'orientation de la base \(b_1\) par rapport à la base \(b_0\) sera ainsi obtenue par des orientations successives de bases dont l'un des vecteurs (correspondant à l'axe de la liaison) sera commun.
Un seul angle suffira alors, à chaque fois, pour "passer" d'une base à une autre. Cette rotation sera représentée graphiquement par une figure plane appelée figure de changement de base.
Fondamental : Figure de changement de base
Soit une base \(b_3\) orientée d'un angle \(\theta\) par rapport à une base \(b_2\) ; le vecteur \(\vec z\) est commun aux deux.
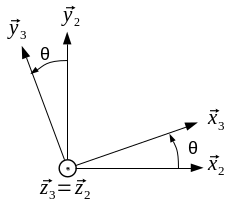
N'importe quelle orientation de base pourra être représentée de la manière ci-dessus en respectant :
le trièdre direct
le vecteur commun "sortant" du plan vers le lecteur
un angle positif faible
Attention :
La figure précédente peut être déduite de la définition suivante : \(\theta= (\vec x_2, \vec x_3) = (\vec y_2, \vec y_3)\).
La figure de changement de base permet de représenter de façon plane un paramètre d'orientation et les deux bases qui lui sont reliées.
Elle est d'une importance capitale pour la projection correcte des vecteurs des différentes bases.
Remarque :
Plusieurs figures de changement de base seront peut-être nécessaires (parfois quatre, cinq, etc..) pour décrire toutes les orientations successives permettant d'orienter un solide par rapport à un autre.
A chacune correspondra un paramètre angulaire.
N'oublions pas qu'en théorie seuls trois angles suffisent (cf. angles d'Euler).
Méthode : Tracer une figure de changement de base
La méthode suivante correspond à l'angle défini comme suit : \(\theta_2 = \left( \vec z_1, \vec z_2 \right) = \left( \vec x_1, \vec x_2 \right)\)
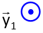
On repère l'axe de la liaison (ici \(\vec y_{1, 2}\) selon la définition de l'angle \(\theta_2\)), et on le trace "venant vers soi".
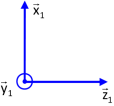
On trace ensuite la base de référence (ici base 1), en faisant attention à ce que le trièdre tracé soit bien direct.
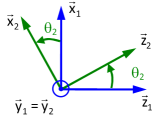
Enfin, on trace la base d' "arrivée" (ici base 2), en veillant à ce que l'angle soit tracé dans le premier cadran, quels que soient sa valeur ou son signe sur le schéma cinématique.